Neural Peripheral Device Modeling

Introduction

Black-box learning involves trying to learn as much as you can about how a system functions based solely on observations of the inputs to the system and the resulting outputs. This problem is unsolvable in the general sense, but
remains relevant and interesting to a wide variety of problem spaces.

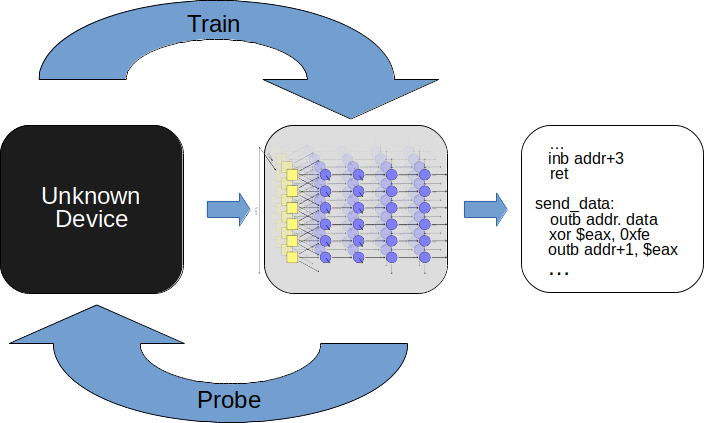
Traditional black-box learning systems rely on learning an exact automata of the system, and use grammatical inference to try to exactly model the device’s internal state. These systems are limited in value in that the algorithmic complexity of the system is exponential to the number of internal states of the system. State of the art algorithms are limited to systems with only ~200 internal states¹.

Our key observation in this research is that input/output observation pairs look a lot like training set data for machine learning. Instead of trying to learn an exact model of the system under test, can we instead train a recurrent neural network using the observations to develop a functionally equivalent model to the real system. In essence, we replace the “black box” with a functionally equivalent “opaque box” of a trained neural network. The observed internal state machine of the black box, which can not be observed directly, is then encoded in the structure and weights of the trained recurrent network model, which are observable and provide valuable insight into how the original device works.

Since we’re only learning a fuzzy approximation of the original model, we side-step the computational complexity issues with traditional grammatical inference methods, while maintaining enough fidelity for a wide range of tasks.

Publications

• “Learning Device Models with Recurrent Neural Networks”, J. Clemens, IJCNN 2018.
  [ paper | slides | arXiv | jupyter | bibtex ]

Source Code

Official source code for dataset generation and examples of network creation is available on GitLab:

[https://gitlab.com/clemej/neurodev-models](https://gitlab.com/clemej/neurodev-models)

References